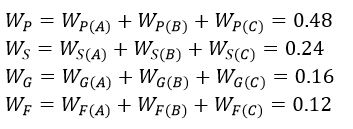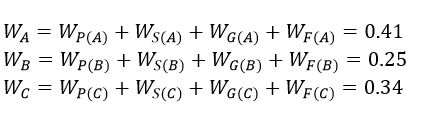Ordinal Priority Approach (OPA)

Multiple-Criteria Decision Analysis

Do you know the common challenges in the Multiple-Criteria Decision Analysis field?
  • Problems associated with using pairwise comparison matrix.
  • Problems associated with using normalization.
  • Problems stemming from collecting quantitative data.
  • Problems associated with using averaging methods for aggregating experts’ opinions.
  • Judgement without possessing sufficient knowledge.
  • Problems resulting from positive and negative ideal solutions.


Multiple-Criteria Decision Analysis

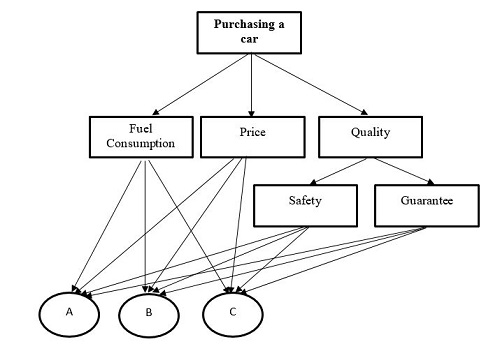
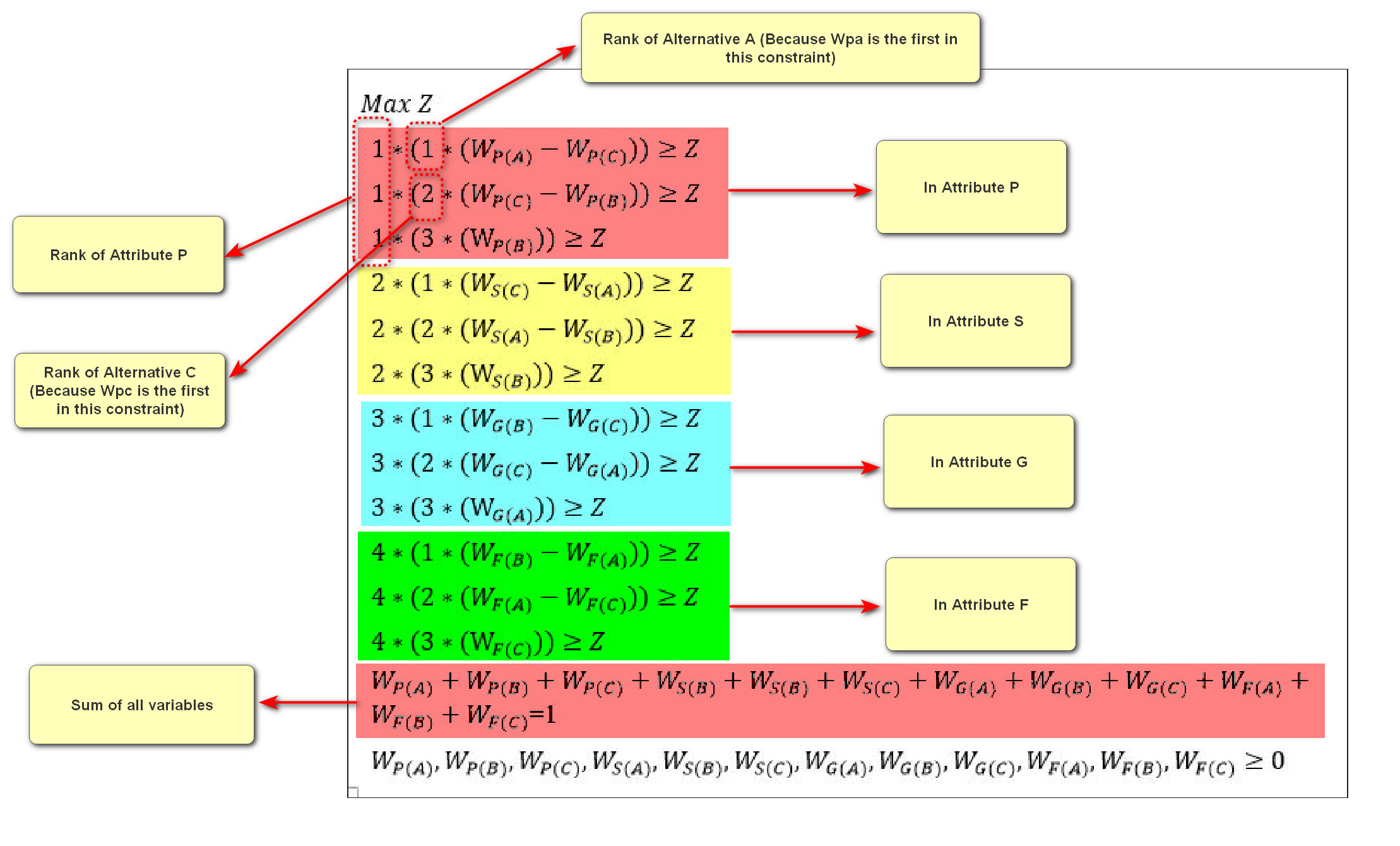
Multiple-Criteria Decision Analysis (MCDA) is a common problem in real-life situations. This problem has three important elements, including experts, criteria, and alternatives. When there is a need to make a decision, the Multiple-Criteria Decision Analysis methods can help us. For example, when we want to decide which car is suitable to buy, it is a decision-making problem that can be solved using Multiple-Criteria Decision Analysis methods. For buying a car, criteria can be price, quality, comfort, etc. The available cars can be defined as alternatives. One of the most recent Multiple-Criteria Decision Analysis methods is the Ordinal Priority Approach. It can consider the three important elements of decision problem simultaneously which makes it different from other existing methods. There are several software which can solve the Multiple-Criteria Decision Analysis problems using the Ordinal Priority Approach at the speed of light.


Web-Based Software for Multiple-Criteria Decision Analysis Problems

To facilitate the process of solving Multiple-Criteria Decision Analysis Problems using the Ordinal Priority Approach, a web-based solver is provided. This software has no limitations regarding the number of experts, criteria, and alternatives. It is easy to use and freely available for scholars who want to use the Ordinal Priority Approach in Multiple-Criteria Decision Analysis Problems. The following Figure shows the Web-Based Software for Multiple-Criteria Decision Analysis Problems.

Web-Based Software for Multiple-Criteria Decision Analysis Problems


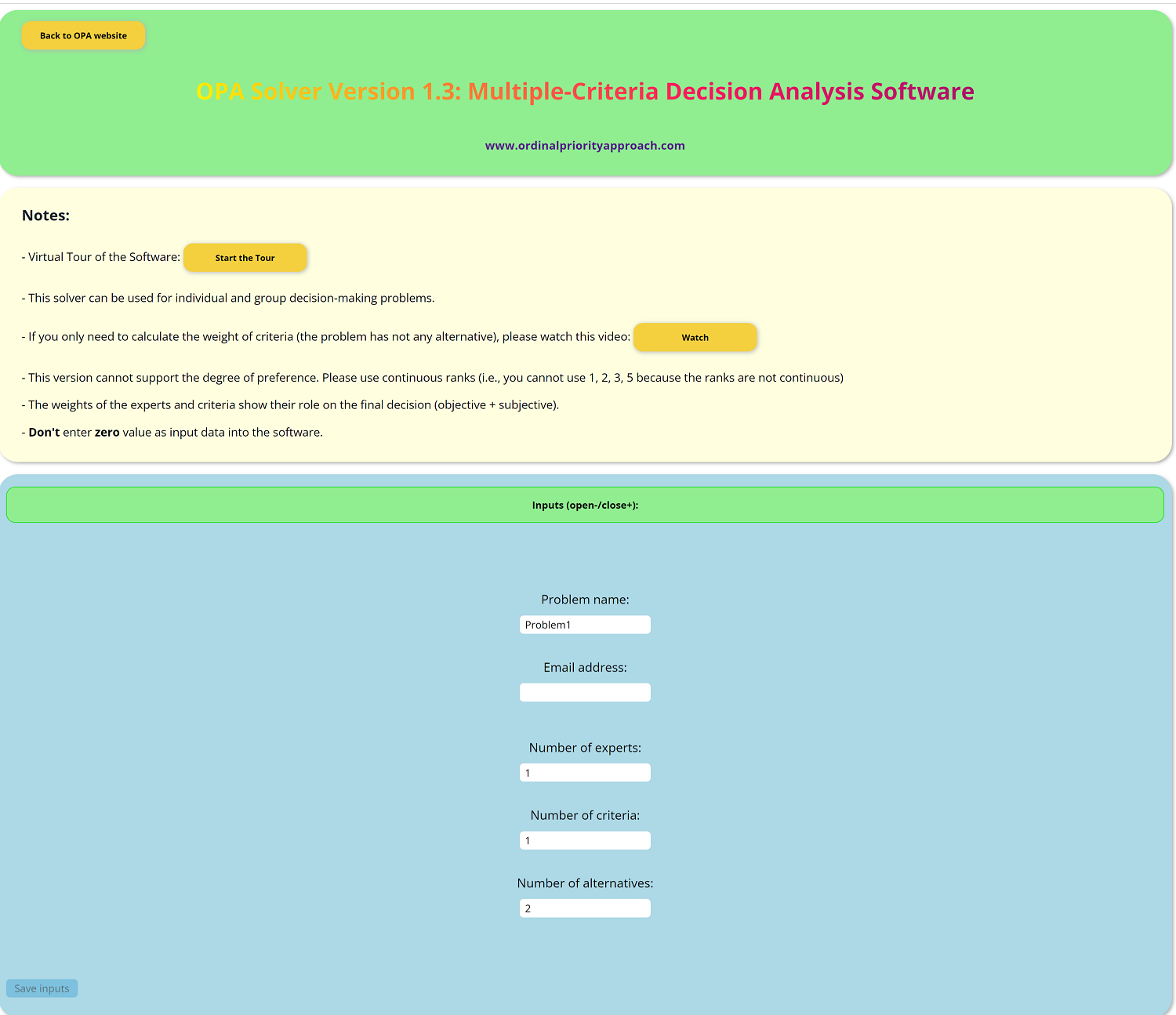
Link to the Software : Web-Based Software for Multiple-Criteria Decision Analysis Problems


Excel-Based Software for Multiple-Criteria Decision Analysis Problems

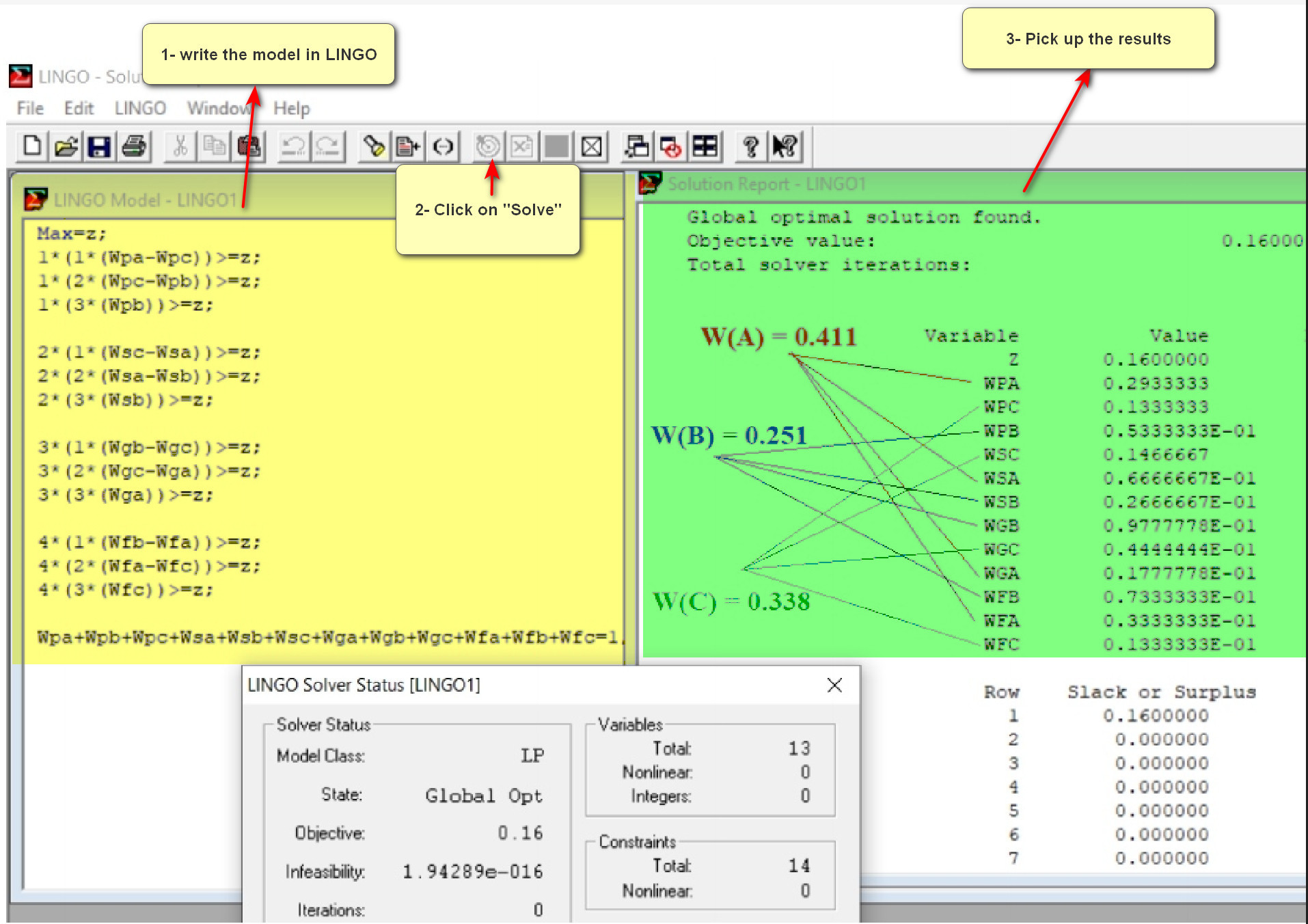
To solve Multiple-Criteria Decision Analysis Problems using the Ordinal Priority Approach, there are Excel-based, Web-based software, and MATLAB-based solver. The Excel-based software is useful for small-size problems of Multiple-Criteria Decision Analysis because the Solver of the Excel is limited and cannot handle a lot of constraints. The Excel-based solver is very easy to use and fast. It can solve the Multiple-Criteria Decision Analysis problems at the speed of light.

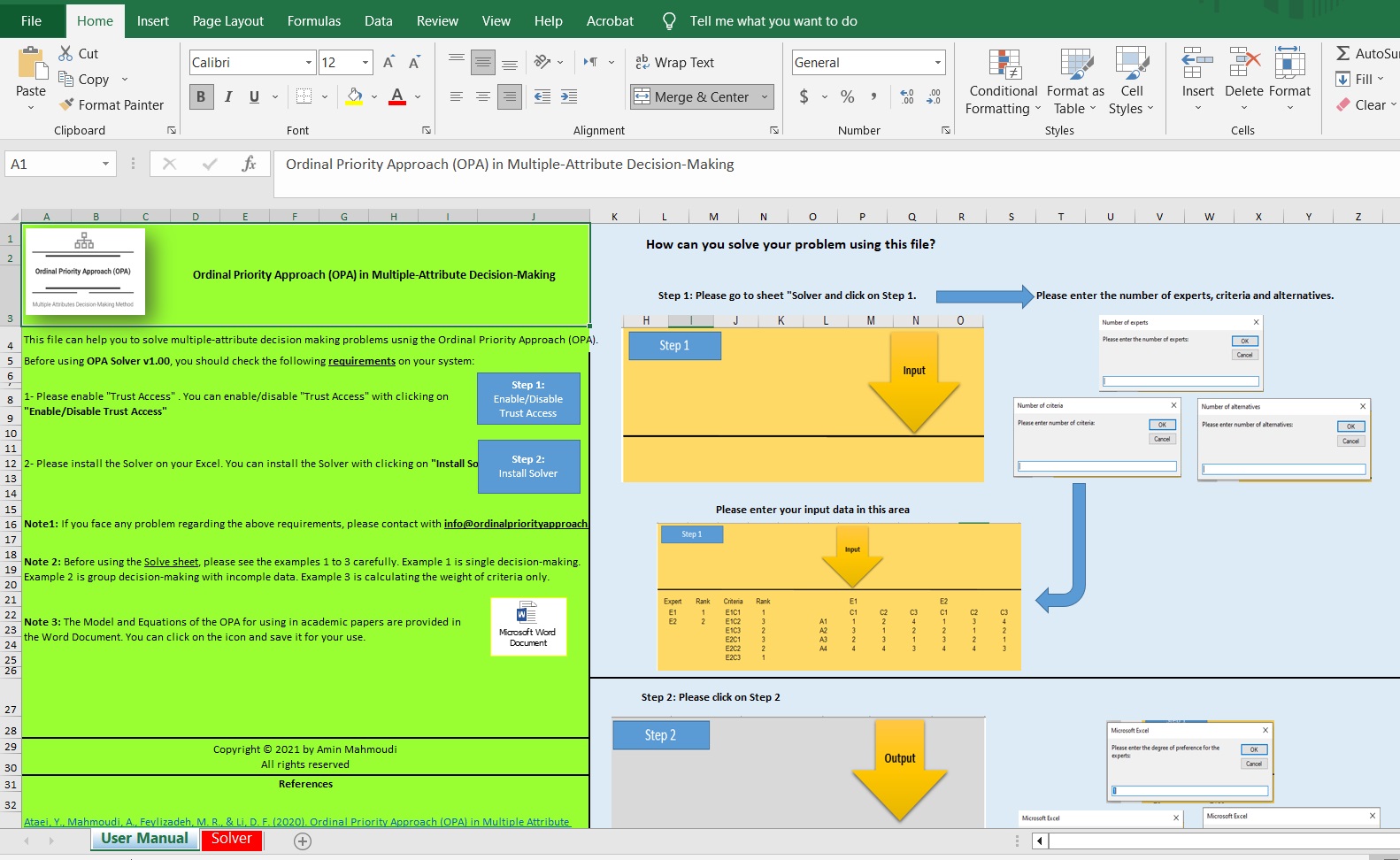
Multiple-Criteria Decision Analysis

Link to the Software : Excel-Based Software for Multiple-Criteria Decision Analysis Problems


MATLAB-Based Software for Multiple-Criteria Decision Analysis Problems

To solve Multiple-Criteria Decision Analysis Problems using the Ordinal Priority Approach, there are Excel-based, Web-based software, and MATLAB-based software. The MATLAB-based software is useful for large-scale problems of Multiple-Criteria Decision Analysis. The MATLAB-based solver has user manual file, which can facilitate the process of solving the problem.

MATLAB-Based Software for Multi-Criteria Decision Analysis Problems


Link to the Software : MATLAB-Based Software for Multiple-Criteria Decision Analysis Problems


Solving an Example Using the OPA

Here, we are going to solve the first example from Ordinal Priority Approach (OPA) in Multiple-Criteria Decision Analysis for the scholars who want to employ the OPA in their papers. This example is related to purchasing a car by considering the following attributes:

Multiple-Criteria Decision Analysis

It should be noted that there are three alternatives entitled A, B, and C. After identifying the attributes and alternatives, we should collect the data from the expert. The input data for this example are as follows:

Rank of attributes: P > S > G > F

The rank of alternatives:

In attribute P: A > C > B

In attribute S: C > A > B

In attribute G: B > C > A

In attribute F: B > A > C

As can be seen from the above table, the expert declared that the order of the attributes is P=1, S =2, G =3, F=4. Moreover, the order of the alternatives in each attribute was provided. For example, in attribute P, we have A=1, C=2, B=3. After collecting data, the OPA model should be constructed as follows:


Multiple-Criteria Decision Analysis

This is a linear model which can be solved using various software such as GAMS, LINGO, Excel, etc. Here, we used LINGO software:




Then, the weight of the attributes can be calculated as follows:


Multiple-Criteria Decision Analysis

Likewise, the weight of the alternatives can be calculated as follows:


Multiple-Criteria Decision Analysis